- Posts: 4403
curve smoothing
- PhracturedBlue
-
Topic Author
- Offline
I am curious how folks will feel if you can only use 11-point (or less) curves with smoothing?
Adding more fields to the curve structure has a large impact on memory usage. the alternative of not pre-calculating the control-points has a potential performance impact.
On the Devo8/10/12 we have lots of RAM so I could pre-calculate the control-points without issue.
On the Devo7e, I'm in a bind because I don't want to increase memory allocation.
So my options are:
1) not support curve-smoothing on the 7e
2) do something special for the 7e (support fewer mixers or curve-points)
3) be consistent and limit all models to 9-point curves when using smoothing
4) increase the memory usage on the devo7e (probably limiting other capabilities in the future)
5) do-not pre-caclulate and hope we have enough spare cycles to not impact the system
I really don't like option (2) or (5) but I'm not sure what the best solution is here. I'm leaning towards (1) since I don't really want the devo7e to prevent me from developing features for the other radios, but I know a lot of folks use it, and this is one of the most-requested features.
Assuming you build from source, from the 'src' dir, run:
patch -p2 < path_to_bezier_patch_file
Please Log in or Create an account to join the conversation.
- clearprop88
-
- Offline
- Posts: 94
Please Log in or Create an account to join the conversation.
- Hexperience
-
- Offline
- Posts: 588
4) I don't have a 7e, so take this with that in mind, but why "save" the memory for an as yet unknown feature in the future? I'm sure you have plans for the memory usage, but if the 7e users know what they may loose they can make an informed decision. i.e. They can have 9 point smoothing, but will loose X. They may want X more than Y...
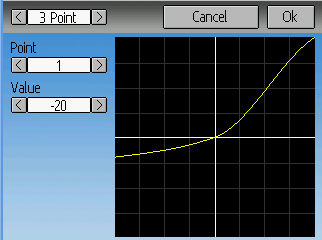
Question though.. Let's say I have a 3 point "curve" -20,0,+100. How would that smooth? I want a straight line from -20 to 0 and another straight line from 0 to +100. Would the smoothing only apply to 5 point curves and higher?
There are 10 types of people in this world. Those that understand binary and those that don't.
Please Log in or Create an account to join the conversation.
- PhracturedBlue
-
Topic Author
- Offline
- Posts: 4403
Please Log in or Create an account to join the conversation.
- PhracturedBlue
-
Topic Author
- Offline
- Posts: 4403
Please Log in or Create an account to join the conversation.
- vlad_vy
-
- Offline
- Posts: 3333
Please Log in or Create an account to join the conversation.
- richardclli
-
- Offline
- Posts: 199
Anyway, I will try to look into it and see if there are any better choices.
Please Log in or Create an account to join the conversation.
- sbstnp
-
- Offline
- Posts: 649
richardclli wrote: I don't cubic spline is suitable for this kind of curve fitting, since cubic function will have overshoot effect. I think something like parabolic/exponential fitting function may fit better.
Anyway, I will try to look into it and see if there are any better choices.
Yeah this is known.
Devo 10 + 4in1
FrSky Taranis + TBS Crossfire
Please Log in or Create an account to join the conversation.
- PhracturedBlue
-
Topic Author
- Offline
- Posts: 4403
I guess I should have clarified that it is a cubic bezier spline (which has control points in the 1st place, and not some sort of cubic-fit.
Please Log in or Create an account to join the conversation.
- vlad_vy
-
- Offline
- Posts: 3333
Please Log in or Create an account to join the conversation.
- richardclli
-
- Offline
- Posts: 199
-x'.sinθ + y'.cosθ = a.(x'.cosθ + y'.sinθ)² + b.(x'.cosθ + y'.sinθ) + c
and need to solve this formula using 2 points with 2 slopes on the points. This should give a good effect, but I need somebody good at geometry to solve all the four variables out of 2 points and 2 slopes.
What do you think?
Please Log in or Create an account to join the conversation.
- PhracturedBlue
-
Topic Author
- Offline
- Posts: 4403
I figured out why vlad was seeing curvature in what should be a straight line. I made the simplifying assumption that f(t) is ~= f(x) which is a terrible assumption. Unfortunately it also means that the whole thing may be bunk, since calculating t from x may require a solver that i don't want to implement.
Please Log in or Create an account to join the conversation.
- PhracturedBlue
-
Topic Author
- Offline
- Posts: 4403
It has several benefits:
1) it can be directly calculated as f(x) which makes it much better suited to our needs (straight-line performance is now good)
2) there are monotone rules for calculating the tangents to guarantee no overshoot. These are better formalized than the home-brew rules I developed for the bezier curve
This was the function that was originally recommended to me in the bitbucket ticket, but I completely missed that it works fine with local maxima.
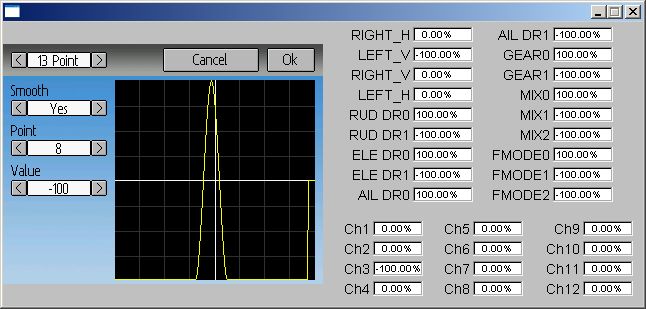
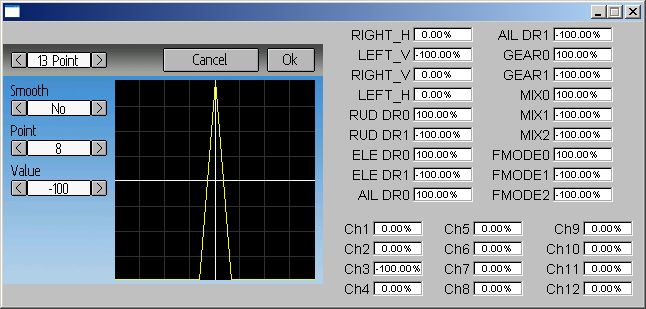
Anyhow, let me know how it works. I still haven't looked into why the 13-pointcurve isn't functioning right. It is definitely a bug, but I don't think it is directly related to the curve properties.
Please Log in or Create an account to join the conversation.
- PhracturedBlue
-
Topic Author
- Offline
- Posts: 4403
Please Log in or Create an account to join the conversation.
- richardclli
-
- Offline
- Posts: 199
Please Log in or Create an account to join the conversation.
- PhracturedBlue
-
Topic Author
- Offline
- Posts: 4403
en.wikipedia.org/wiki/Monotone_cubic_interpolation
The only significant change I made was to not calculate Beta but instead use mk/deltak+1 to enforce the monotonic behavior, since that is what I had available. this may not work perfectly, but so far it seems to be working as expected.
Please Log in or Create an account to join the conversation.
- vlad_vy
-
- Offline
- Posts: 3333
Please Log in or Create an account to join the conversation.
- RandMental
-
- Offline
- Posts: 521
PhracturedBlue wrote: I still haven't looked into why the 13-pointcurve isn't functioning right. It is definitely a bug, but I don't think it is directly related to the curve properties.
Hi PB,
I had noticed a problem with a 13 point setting a few weeks ago. It was with V3.0.0 and a well formed throttle curve (a valid curve for a heli) but when this model was selected there was almost a 1 second delay on the throttle response, both on the heli and on the bar on the main page. I changed back to a 7 point curve and no more delay. I haven tried revisit or duplicating it yet, 7 points are all I need, but I thought mentioning it while you are looking at the curve smoothing and memory use.
On an earlier question - at least for Helicopters, 9 points curves are plenty and would be my vote if needed to reduce memory requirements.
Please Log in or Create an account to join the conversation.
- PhracturedBlue
-
Topic Author
- Offline
- Posts: 4403
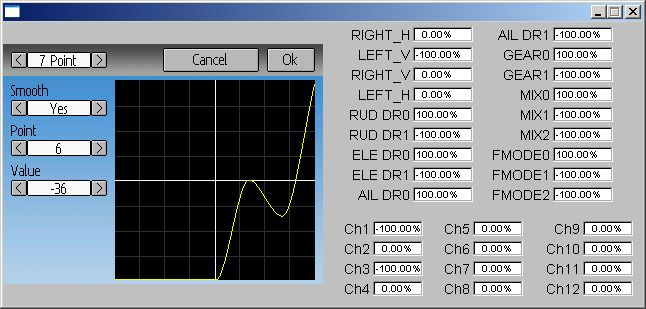
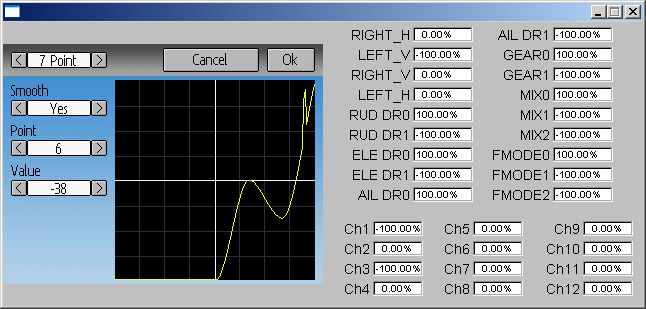
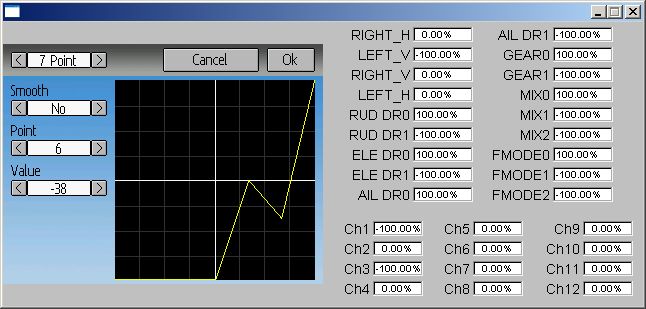
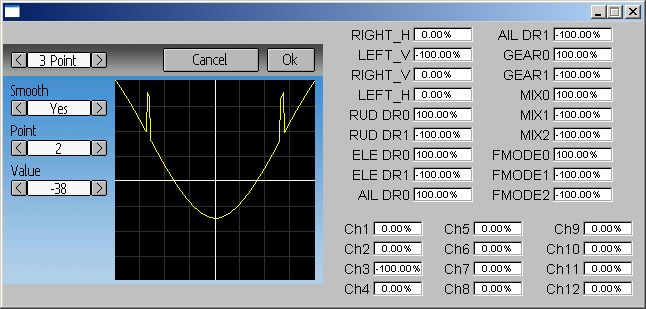
Thanks vlad. Calculating these splines in only 32bits without any overflow requires very careful management of multipliers. I had the order of operations slightly wrong and that was allowing the values to overflow. I've applied a fix that corrects this. Let me know if you see more issues.vlad_vy wrote: I found other artifact, spike on curve:
If point 6 value will be lower, spike on curve can overshoot 100%. It has place only with first ans last segment of curve.
Please Log in or Create an account to join the conversation.
- vlad_vy
-
- Offline
- Posts: 3333
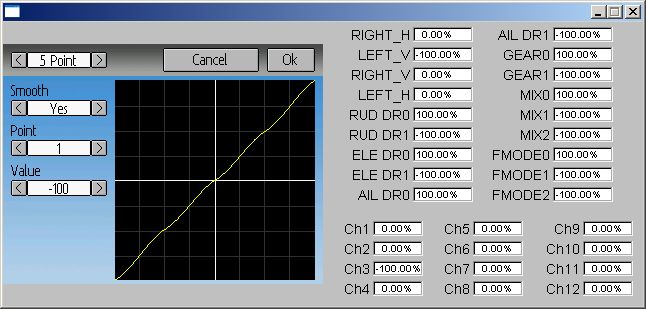
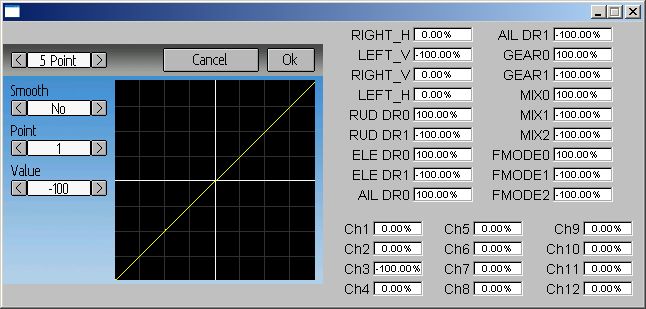
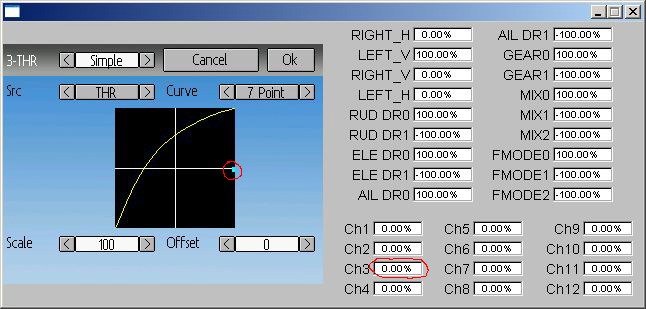
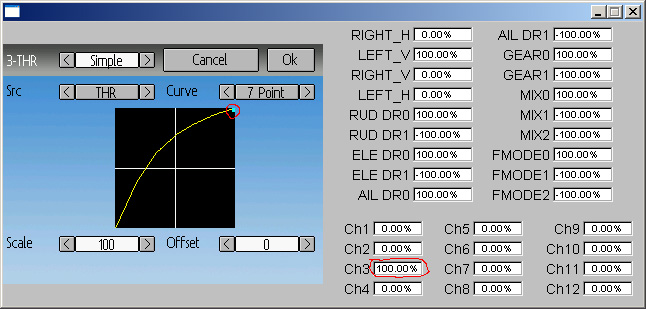
7 point curve, throttle (ch3), -100, -25, 25, 55, 75, 90, 100. If throttle (Ch3) = 100%, at channel monitor Ch3 = 0% (and at right panel of emulator). Any decrease and Ch3 value restored. If curve smooth = Off, all works as expected.
Smoothed curve
Curve without smoothing
Please Log in or Create an account to join the conversation.
-
Home

-
Forum

-
General

-
General Discussions

- curve smoothing